문제 링크
https://www.acmicpc.net/problem/16480
16480번: 외심과 내심은 사랑입니다
수진이는 외심과 내심 없이는 살 수 없다고 말할 정도로 외심과 내심을 사랑한다. 하지만, 갑자기 수진에게 어려운 일이 닥쳤다. 바로 평면에 있는 삼각형 ABC에서 외접원의 반지름의 길이 R이고,
www.acmicpc.net
아이디어
오일러 삼각형 정리를 아는지 묻는 기하문제이다.
위 정리는 삼각형의 외심과 내심 사이의 거리를 외접원과 내접원의 반지름을 통해 나타내는 정리이다.
d : 외심과 내심 사이의 거리
R : 외접원의 반지름
r : 내접원의 반지름
오일러 삼각형 정리는 각 변수를 위와 같이 정의할 때 다음과 같다.

오일러 삼각형 정리 증명
오일러 삼각형 정리의 증명에 쓰이는 "방멱정리"와 "맨션정리"를 먼저 살펴보자.
1. 방멱정리
평면 위에 원이 있고, 내부의 점 P가 주어졌을 때,
점 P를 지나는 한 직선이 원과 만나는 점을 각각 A, C
점 P를 지나는 또 다른 직선이 원과 만나는 점을 각각 B, D라고 할 때, 다음과 같다.


맞꼭지각과 동위각에 의해 AA닮음인 삼각형 쌍을 발견하며, 닮음비를 세워 방멱정리를 증명할 수 있다.




2. 맨션정리
삼각형 ABC의 외접원 O와 내심 I에 대해, 직선 AI와 외접원 O가 만나는 A와 다른점을 D라 할 때,
BD=CD=DI가 성립한다.

각 IAB, IBC, ICA를 각각 x, y, z라고 할 때, 내심의 성질에 의해서 각 IAC, IBA, ICB의 값을 알 수 있다.
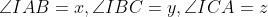

호 BD의 원주각과 호 CD의 원주각이 모두 같음을 알 수 있다.

각 BID는 삼각형 AIB의 외각이며, 각 CID는 삼각형 AIZ의 외각이다.

삼각형의 두 각이 크기가 같으므로 이등변 삼각형이며 두 변의 길이가 같음을 알 수 있다.



오일러 삼각형 정리

외심 O와 내심 I를 연결한 직선이 외접원과 만나는 점을 각각 P, Q
삼각형의 한 점 A에서 내심 I에 연결한 직선이 외접원과 만나는 점을 D라고 하자.
위의 그림에서 방멱정리에 따라 다음과 같은 식이 성립한다. 이 식을 각 선분의 길이인 R, r, d로 나타내보자.




이 때, 맨션 정리에 의해 CD의 길이와 ID의 길이가 같으므로

식1에 각 선분의 길이를 대입하여 최종적으로 오일러 삼각형 정리를 유도하자.



소스코드
#include <cstdio>
int main()
{
long long R, r;
scanf("%lld %lld", &R, &r);
printf("%lld",R*(R-2*r));
return 0;
}
R, r <= 100,000 이므로 overflow를 조심해야 합니다.
+
방멱정리 그 자체인 간단한 문제
https://www.acmicpc.net/problem/16478
16478번: 원의 분할
장난꾸러기 혁주는 어렸을 때부터 가위를 아주 잘 다루었다. 그래서 그는 색종이를 가위로 아무렇게나 자르는 것을 좋아한다. 혁주는 오늘 친구에게 원 모양의 색종이를 생일 선물로 받았다. 그
www.acmicpc.net
공부한 것을 정리하기 위한 기록입니다.
틀린 부분이 있다면 언제나 부드럽게 알려주세요.
'PS > BOJ' 카테고리의 다른 글
| [BOJ 16890] 창업 (0) | 2020.08.31 |
|---|---|
| [BOJ 1310] 달리기 코스 (0) | 2020.08.26 |
| [BOJ 18870] 좌표 압축 (0) | 2020.07.16 |
| [BOJ] 어른 상어 (0) | 2020.06.09 |
| [BOJ 19236] 청소년 상어 (0) | 2020.06.09 |


댓글